PhysLab.net – Pendulum and Cart

In this simulation there is a cart moving along a horizontal track. From the cart a pendulum is suspended. A spring connects the cart to a wall. Friction acts on the cart and on the pendulum.
You can change parameters such as gravity, mass, pendulum length, spring stiffness, and friction (damping). You can drag the cart or pendulum with your mouse to change the starting position. Click the "reset" button to start from a resting position. If you don't see the simulation try instructions for enabling Java. Scroll down to see the math!

There are two ways to find the equations of motion for a system like this: the direct Newtonian way or the indirect Lagrangian way. We show both methods here.

Kinematics

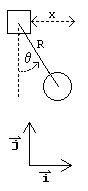
diagram of cart & pendulum variables and i, j unit vectors

For both direct and indirect methods, we first need to get the kinematics right. Kinematics means the relations of the parts of the device, without regard to forces. In kinematics we are only trying to find expressions for the position, velocity, & acceleration in terms of whatever variables we have chosen. The variables here are:

x = position of cart (0 = spring unstretched)
θ = angle of pendulum (0 = pendulum hanging straight down)
R = length of rod (constant)

We'll need the standard unit vectors, i, j, k. We use bold and overline to indicate a vector.

i = (1,0,0) unit vector in horizontal direction
j = (0,1,0) unit vector in vertical direction
k = (0,0,1) unit vector in z direction (out of the page)

The kinematics for the cart are simple position = x i
velocity = x' i
acceleration = x'' i
The kinematics for the pendulum are more complex. The position is derived by a fairly simple application of trigonometry. The velocity and acceleration are then the first and second derivatives of the position. position = x i + R sin θ i − R cos θ j velocity = x' i + R θ' cos θ i + R θ' sin θ j acceleration = x'' i + R θ'' cos θ i − R θ' ² sin θ i + R θ'' sin θ j + R θ' ² cos θ j

Forces

We treat the cart and the pendulum bob as point particles. Begin by drawing the free body diagram for the cart and writing expressions for the forces acting on them. Define the following parameters and forces:

N = normal force (from the track the cart is on)
T = tension in the rod
M = mass of cart
m = mass of pendulum
g = gravitational constant
d = cart friction constant
b = pendulum friction constant
k = spring stiffness

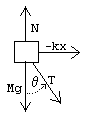cart forces

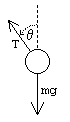
pendulum forces

Just by looking at the free-body diagram we can fairly easily figure out some of the forces on the cart. (The pendulum friction force is trickier, it's explained in the next section).

spring force = −k x i
normal force = N j
gravity = −M g j
tension in the rod = −T cos θ j + T sin θ i
cart friction = −d x' i
pendulum friction = ^b⁄_R θ' (cos θ i + sin θ j)

The forces on the pendulum bob are:

tension in the rod = T cos θ j − T sin θ i
gravity = −m g j
pendulum friction = −^b⁄_R θ' (cos θ i + sin θ j)

Torque Force from Pendulum Friction

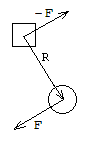
torque force of friction

We consider the torque from friction of the pendulum to be a vector perpendicular to the plane where the pendulum and cart move. That is, the torque is in the direction of the unit vector k which extends out of the plane. The magnitude of the torque is given by −b θ' where θ' is the angular velocity. We can regard the force from the torque as being equivalent to a force applied at the end of the pendulum rod (see illustration). From Newton's Third Law (every action has an equal and opposite reaction) we know that the same force is applied at the other end of the rod, but in opposite direction.

A torque that is the result of a force F applied at the end of the rod R is given by the cross product R × F = (R_x, R_y, 0) × (F_x, F_y, 0) = (R_x F_y − R_y F_x) k Here we are showing a 3-space vector as (x, y, z) which is the same as x i + y j + z k. We regard the force F as being perpendicular to the rod, so that F = f (−R_y, R_x, 0) ⁄ R where f is the unknown magnitude of F and R is the length of R so that R = √(R_x² + R_y²). The direction of F is chosen so that positive torque leads to increase in θ. Then the cross product becomes R × F = (R_x F_y − R_y F_x) k = f (R_x² + R_y²) ⁄ R k = f R k Now we can find f: −b θ' k = R × F = f R k f = ^−b⁄_R θ'
This result makes sense: consider that to produce a given amount of torque, you would need a stronger force applied at the end of a short rod, or a weaker force with a longer rod. The force is then given by F = f (−R_y, R_x, 0) ⁄ R = ^−b⁄_R θ' (cos θ i + sin θ j) Note that R = R(sin θ, −cos θ, 0) which justifies part of the above equation. This torque force F is applied at the pendulum bob, and its opposite is applied at the cart.

Direct Method for Finding Equations of Motion

We add up the forces described above to find the net force on the cart F = N j − M g j − T cos θ j + T sin θ i − k x i − d x' i + ^b⁄_R θ' (cos θ i + sin θ j) Now using Newton's law F = M a and the cart acceleration we found earlier, we have

N j − M g j − T cos θ j + T sin θ i − k x i + ^b⁄_R θ' (cos θ i + sin θ j) = M x'' i

(1)

Adding the forces on the pendulum gives F = T cos θ j − T sin θ i − m g j − ^b⁄_R θ' (cos θ i + sin θ j) Using Newton's law F = m a and the pendulum acceleration we found earlier, we have

T cos θ j − T sin θ i − m g j − ^b⁄_R θ' (cos θ i + sin θ j) = m(x'' i + R θ'' cos θ i − R θ' ² sin θ i + R θ'' sin θ j + R θ' ² cos θ j)

(2)

Now we can write the vector components of the above equations (1) and (2) as separate equations. This gives us 4 simultaneous equations.

T sin θ − k x − d x' + ^b⁄_R θ' cos θ = M x''

(3)

N − M g − T cos θ + ^b⁄_R θ' sin θ = 0

− T sin θ − ^b⁄_R θ' cos θ = m(x'' + R θ'' cos θ − R θ' ² sin θ)

(4)

T cos θ − m g − ^b⁄_R θ' sin θ = m(R θ'' sin θ + R θ' ² cos θ)

(5)

(We ignore the second of the four equations, but we could use it to find the unknown normal force N on the cart). Next do some algebraic manipulations to eliminate the unknown tension T. Adding together equations (3) and (4) and rearranging we get:

(M + m)x'' = m R θ' ² sin θ − m R θ'' cos θ − k x − d x'

(6)

Multiply equation (5) by sin θ T sin θ cos θ − m g sin θ − ^b⁄_R θ' sin² θ = m R θ'' sin² θ + m R θ' ²sin θ cos θ Use equation (4) to replace T sin θ. −^b⁄_R θ' cos² θ − m x'' cos θ − m R θ'' cos²θ + m R θ' ²sin θ cos θ − m g sin θ − ^b⁄_R θ' sin² θ = m R θ'' sin²θ + m R θ' ²sin θ cos θ Using the trig identity cos²θ + sin²θ = 1 this simplifies to

^b⁄_R θ' + m x'' cos θ + m R θ'' + m g sin θ = 0

(7)

Equations (6) and (7) are the equations of motion. We have two equations in the two variables x,θ and their derivatives. We will need to do some further manipulations of these two equations to get them into a form suitable for the Runge-Kutta numerical analysis method (see below).

Indirect (Energy) Method for Finding Equations of Motion

The indirect method is based on the energy of the system. (A good textbook that covers this is Fundamentals of Applied Dynamics by James H. Williams Jr. You will find the same "Mass and Plane Pendulum Dynamic System" discussed on page 234 of the 1996 edition.) Our first step is to find the Lagrangian of the system which is the kinetic energy minus the potential energy. L = T − V

L = the Lagrangian
T = kinetic energy
V = potential energy

For the kinetic energy we need the velocity of the cart and pendulum, which we calculated earlier (see kinematics above). Kinetic energy is given by ¹⁄₂m v². Note that we use the vector dot product to square a vector, v² = v · v. So we have T = ¹⁄₂ M (x' i)² + ¹⁄₂ m (x' i + R θ' cos θ i + R θ' sin θ j)² Applying the dot product rule to square the vectors we get T = ¹⁄₂ M x' ² + ¹⁄₂ m ((x' + R θ' cos θ)² + (R θ' sin θ)²)
There are two stores of potential energy in this system: the spring and the gravitational potential of the pendulum. V_spring = ¹⁄₂ k x² V_gravity = m g height = m g(R − R cos θ) So the Lagrangian for the system is L = ^M⁄₂ x' ² + ^m⁄₂ (x' + R θ' cos θ)² + ^m⁄₂ (R θ' sin θ)² − ^k⁄₂ x² − m g R(1 − cos θ)

Generalized Forces: Friction

To deal with the friction forces we calculate the amount of non-conservative work done by tiny movements in the variables. Note that we consider only non-conservative forces like friction here -- conservative forces like gravity or springs are handled by the potential energy calculations in the Lagrangian.

A tiny change of Δx in x results in an amount of non-conservative work from friction given by ΔW = −d x' Δx so we define the "generalized force" W_x = −d x' Similarly, a tiny change of Δθ in θ results in an amount of non-conservative work from friction ΔW = −b θ' Δθ, so we define another generalized force: W_Q = −b θ'

Equations of Motion from Lagrangian

Next we will derive the equations of motion from Lagrange's Equation. For the x variable Lagrange's Equation is

W_x = $\frac{d}{dt} \left( \frac{\partial L}{\partial x'} \right) - \frac{\partial L}{\partial x}$

(8)

Note that x' and x are treated as separate variables when taking partial derivatives. Here are the partial derivatives:

∂ L	= M x' + m(x' + R θ' cos θ)
∂ x'

∂ L	= − k x
∂ x

Taking the derivative with respect to time of $\frac{\partial L}{\partial x'}$ and subtracting $\frac{\partial L}{\partial x}$ equation (8) becomes − d x' = M x'' + m x'' + m R θ'' cos θ − m R θ' ² sin θ + k x which we can rearrange to be identical to equation (6) found above in the direct method: (M + m)x'' = m R θ' ² sin θ − m R θ'' cos θ − k x − d x'
For the θ variable Lagrange's Equation is

W_Q = $\frac{d}{dt} \left( \frac{\partial L}{\partial \theta'} \right) - \frac{\partial L}{\partial \theta}$

(9)

Here are the partial derivatives:

∂ L	= m(x' + R θ' cos θ)R cos θ + m θ' R² sin²θ
∂ θ'

∂ L	= −m(x' + R θ' cos θ)R θ' sin θ + m R² θ' ²sin θ cos θ − m g R sin θ
∂ θ

(Notice that we can factor out m R from each of these terms.) Taking the derivative with respect to time of $\frac{\partial L}{\partial \theta'}$ and subtracting $\frac{\partial L}{\partial \theta}$ equation (9) becomes − b θ' = m R [(x'' + R θ'' cos θ − R θ' ² sin θ)cos θ − θ' sin θ(x' + R θ' cos θ) + θ'' R sin²θ + 2 θ' ²R sin θ cos θ + (x' + R θ' cos θ)θ' sin θ − R θ' ²sin θ cos θ + g sin θ] After lots of cancellation and using the identity sin²θ + cos²θ = 1 this reduces to equation (7) from the direct method: ^b⁄_R θ' + m x'' cos θ + m R θ'' + m g sin θ = 0
Which technique do you like better, direct or indirect? It seems that the indirect method is the choice of professionals. It requires more calculus, but the calculations are a lot easier. Compare what was done here to the earlier calculations for frictional torque in the direct method. On the other hand, the direct method is necessary for figuring out the forces within the system, like the tension in the rod, or the normal force of the track on the cart.

Numerical Solution

To solve the equations of motion numerically, so that we can drive the simulation, we use the Runge-Kutta method for solving sets of ordinary differential equations.

To use the Runge-Kutta method, we need to get equations (6) and (7) into the following form: x'' = f(x, x', θ, θ') θ'' = g(x, x', θ, θ') where f, g are functions to be determined. So we want to solve for each second derivative in terms of lower derivative variables. If you look back at equations (6) and (7), you can see that they need some manipulation to isolate the second derivatives over to the left hand side. After solving for θ'' and x'' (either by hand or with an algebra program like Mathematica) we get:

x'' =	m R θ' ² sin θ + m g sin θ cos θ − k x − d x' + ^b⁄_R θ' cos θ
	M + m sin²θ

θ'' =	−m R θ' ² sin θ cos θ − (m+M)g sin θ + k x cos θ + d x' cos θ − (1 + ^M⁄_m)^b⁄_R θ'
	R (M + m sin²θ)

If we define a couple of new variables, we can change this into four first-order equations (that is, four equations with only first derivatives).

v = velocity of cart
ω = angular velocity of pendulum

x' = v θ' = ω

v' =	m R ω² sin θ + m g sin θ cos θ − k x − d v + ^b⁄_R ω cos θ
	M + m sin²θ

ω' =	−m R ω² sin θ cos θ − (m+M)g sin θ + k x cos θ + d v cos θ − (1 + ^M⁄_m)^b⁄_R ω
	R (M + m sin²θ)

This is now exactly the form needed to plug in to the Runge-Kutta method for numerical solution of the system.