PhysLab.net – Double Spring 2D

This simulation shows a two masses connected by springs and suspended from the ceiling. The masses are able to move in 2 dimensions, and gravity operates.
You can drag either mass with your mouse. You can also drag the top anchor point. Click the "reset" button to put the masses in a resting equilibrium. You can change parameters such as gravity, mass, spring stiffness, and friction (damping). If you don't see the simulation try instructions for enabling Java. Scroll down to see the math!

Physics

An immoveable (but draggable) anchor point has two spring2 and bobs hanging below and swinging in two dimensions. We regard the bobs as point masses. We label the upper spring and bob as number 1, the lower spring and bob as number 2.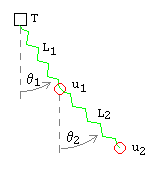

double spring variables

Define the following variables:

θ = angle (0=vertical)
S = spring stretch (displacement from rest length)
L = length of spring
u = position of bob
v = u'= velocity of bob
a = u''= acceleration of bob
F = net force on a bob

Define some constants:

R = rest length of spring
T = position of anchor point
m = mass of bob
k = spring constant
b = damping constant
g = gravitational constant

Note that for this simulation the vertical dimension increases downwards.

Here are the equations of motion. The derivation is similar to that given for the single 2D spring. F_1x = m₁ a_1x = −k₁ S₁ sin θ₁ − b₁ v_1x + k₂ S₂ sin θ₂
F_1y = m₁ a_1y = −k₁ S₁ cos θ₁ − b₁ v_1y + k₂ S₂ cos θ₂ + m₁ g
F_2x = m₂ a_2x = −k₂ S₂ sin θ₂ − b₂ v_2x
F_2y = m₂ a_2y = −k₂ S₂ cos θ₂ − b₂ v_2y + m₂ g The spring stretch S_n and angles θ_n are functions of the positions u_n of the bobs as follows: L₁ = √((u_1x − T_x)² + (u_1y − T_y)²)
L₂ = √((u_2x − u_1x)² + (u_2y − u_1x)²)
S₁ = L₁ − R₁
S₂ = L₂ − R₂
cos θ₁ = (u_1y − T_y)/L₁
sin θ₁ = (u_1x − T_x)/L₁
cos θ₂ = (u_2y − u_1y)/L₂
sin θ₂ = (u_2x − u_1x)/L₂

Numerical Solution

To solve the equations of motion numerically, so that we can drive the simulation, we use the Runge-Kutta method for solving sets of ordinary differential equations. We need to convert the four second order equations of motion to eight first order equations. u_1x' = v_1x
u_1y' = v_1y
u_2x' = v_2x
u_2y' = v_2y
v_1x' = −(k₁/m₁) S₁ sin θ₁ − (b₁/m₁) v_1x + (k₂/m₁) S₂ sin θ₂
v_1y' = −(k₁/m₁) S₁ cos θ₁ − (b₁/m₁) v_1y + (k₂/m₁) S₂ cos θ₂ + g
v_2x' = −(k₂/m₂) S₂ sin θ₂ − (b₂/m₂) v_2x
v_2y' = −(k₂/m₂) S₂ cos θ₂ − (b₂/m₂) v_2y + g We keep in mind that the spring stretch S_n and angles θ_n are functions of the position of the bob u_n as given previously.