PhysLab.net – Collisions With Contact

It may surprise you that getting objects to rest on the floor is a challenging problem! This simulation shows rectangular objects colliding in 2 dimensions. It is based on the rigid body collisions simulation, but it deals with steady contact forces where objects press against the floor, the wall or each other.
Click near an object to exert a rubber band force with your mouse. With the keyboard you can control four "thrusters". The keys S,D,F,E control the gray object's thrusters. The keys J,K,L,I -- and also the arrow keys -- control the green object's thrusters. You can also set gravity, elasticity (bounciness), and damping (friction). You can choose from one to six objects. If you don't see the simulation try instructions for enabling Java. Scroll down to see the math!

Try rearranging the blocks so they lean against each other at various angles, or stacking the blocks. You'll see that they are very slippery and hard to get to stack! This is because there is no contact friction in this simulation.

The contact forces are shown as red lines that appear at the corners of the objects. Contact forces come in pairs that are equal and opposite, but only one of each pair is shown here.

About friction and damping: In this simulation, the contacts between objects have no friction whatsoever, so they can slide against each other easily. The damping parameter that you can modify (you may have to click on the "show controls" button to see the damping parameter) has to do with the motion of the objects through the space -- damping makes it as though the objects are moving through a thick syrup, or that there is friction between the background surface and the objects.

Why is this a challenging problem? Contact forces are tricky to figure out. Other forces are much simpler because they only depend on the position of one or two objects. For example, the force of a spring between two objects depends only on the position of the end points of the spring. But the contact forces between objects depends on all the other forces on the objects and how they rest against each other in a rather complex way.

How To Calculate Contact Forces -- Overview

The software (a class called ContactSim) described here for calculating contact forces works closely with software that handles collisions, see Rigid Body Collisions. That software (a superclass called Thruster5) takes care of collisions. As a result there should be no collisions occuring when the contact force code is active, because the collision code detects collisions, backs up in time to just before the collision and applies an appropriate impulse to cause the objects to bounce (it reverses their velocities). The superclass also calculates the effects of external forces acting on the objects such as gravity, thrust, rubber band, and damping. (Interestingly, it is those external forces that cause the contact forces: without them there would be no forces pushing objects into each other.)

The idea is to calculate the exact amount of force needed at each contact to just barely prevent the objects from penetrating. These forces are calculated in the evaluate method of the ContactSim class, which is called repeatedly by the differential equation solver to find the accelerations of the objects. The differential equation solver uses that information to advance the state of the world through time. On entering this evaluate method we are given the current positions and velocities of each object, which is required information for figuring out where contact points are and the geometry of contact forces between objects.

First we find all the resting contacts between objects. The criteria are: a corner must be very close to an edge and moving very slowly (in the direction perpendicular to the edge). Using these criteria, we assemble a list of contact points. For each contact, we store information such as: which are the two objects that are in contact, what is the normal (perpendicular vector) to the edge, where the point of contact is relative to each object, etc.

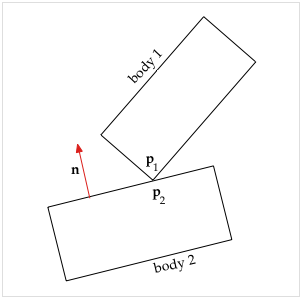
2 bodies in contact

Consider the two objects in contact in the figure. The contact point on body 1 is the corner labeled p₁, the contact point on body 2 is on the edge and labeled p₂. Let d be the distance between the two points, so that d = |p₁ − p₂|. Let n be the normal vector pointing out from body 2 which is perpendicular to the edge. In the diagram below we see the two contact forces that develop at the contact point. There is a contact force f n which acts on body 1 at the point of contact to prevent it from penetrating into body 2. By Newton's 3rd law there is also an equal but opposite force −f n which acts on body 2 at the point of contact to prevent it from penetrating into body 1.

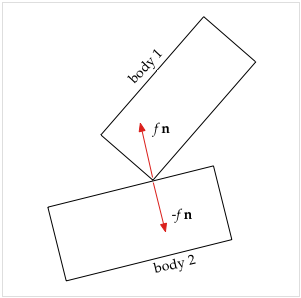
2 bodies with contact forces

What we want to find are the (currently unknown) contact forces, such as f n, which will just barely keep the objects from accelerating into each other, counteracting all the other forces (such as gravity) that are tending to push the objects together.

We focus on the contact distance d, the gap between the points that are in contact. Because the objects are in contact, we have that d = 0 (within numerical tolerance). A value of d < 0 would indicate that the objects are interpenetrating. A value of d > 0 would indicate the objects are not in contact but separated by the distance d.

The rate of change of the contact distance is the velocity d'. Because the objects are in resting contact we have that d' = 0 (within numerical tolerance). This was one of the criteria for selecting the set of resting contact points. Note that the objects can be sliding against each other, because we only care about motion in the direction of the normal (perpendicular to the edge).

What we are most interested in is d'', the acceleration of the gap. Without contact forces we will find that d'' < 0 for most of the contact points, meaning that without any contact force, the objects will fall into each other and interpenetrate.

What makes computing the contact forces somewhat tricky is that they are all interrelated. This is because you can have a complex arrangement of objects resting on each other. The solution involves finding a set of equations that captures exactly how each contact force affects each gap. Then we solve the equations to find forces that exactly set d'' = 0 at each contact point. Actually, we also allow d'' > 0 which means the objects are separating and therefore there is no contact force at that particular contact.

Once we have found the exact force at each contact that will preserve the resting contacts (keeping the objects from accelerating into each other) we then apply those forces to each object. This results in changes to the accelerations of the objects. We then return control to the differential equation solver which continues to evolve the simulation over time using those new accelerations. But now the accelerations are modified so that the objects will remain in resting contact as desired.

Calculating Contact Forces -- in Detail

This software (the ContactSim class) for calculating contact forces is a subclass of the Rigid Body Collisions software (the Thruster5 class). The following description builds on the explanations at that web page, particularly for the external forces. The algorithms used here are based on two papers by David Baraff:

[Baraff-1] David Baraff, An Introduction to Physically Based Modeling: Rigid Body Simulation II - Nonpenetration Constraints. These are lecture notes from Physically Based Modeling: Principles and Practice (Online Siggraph '97 Course Notes).
Note that there is a typographic error on page D62: in several places where you see "a force of j n_j(t₀)" it should read "a force of f_j n_j(t₀)".

[Baraff-2] David Baraff. Fast contact force computation for nonpenetrating rigid bodies. Computer Graphics Proceedings, Annual Conference Series: 23-34, 1994. 12 pages.

Assume that we have a set of n contacts in some particular (but arbitrary) order. Define the following variables:

n = number of contacts.
d_i'' = acceleration of contact distance of the i-th contact.
a = length n vector of accelerations of contact distances, so that a_i = d_i''
f = length n vector of contact force magnitudes (to be determined)
b = length n vector giving contact distance accelerations due to external forces (gravity, thrust, etc.)
A = an n × n matrix that specifies how contact forces affect acceleration of contact distances
a_{i j} = the element of A in the i-th row and j-th column.

Our goal is to set up and solve (subject to certain constraints) the matrix equation

a = A f + b

(1)

The matrix entry a_{i j} tells how much d_i'' changes from a unit change in f_j. If we do the matrix multiplication in equation (1) we see that the acceleration of the i-th contact distance is given by

d_i'' = a_{i 1} f₁ + a_{i 2} f₂ +. . . + a_{i j} f_j + . . . + a_{i n} f_n + b_i

(2)

This says that the acceleration of the i-th contact distance is a function of the contact forces f₁, f₂,..., f_n and the external forces in b_i. We can figure out the a_{i j} and b_i (see below). The d_i'' need to come out zero or positive, because the objects can't accelerate into each other (they are rigid bodies that don't interpenetrate). So the only unknowns are the contact forces f_i, and we can solve this system of simultaneous equations to find them.

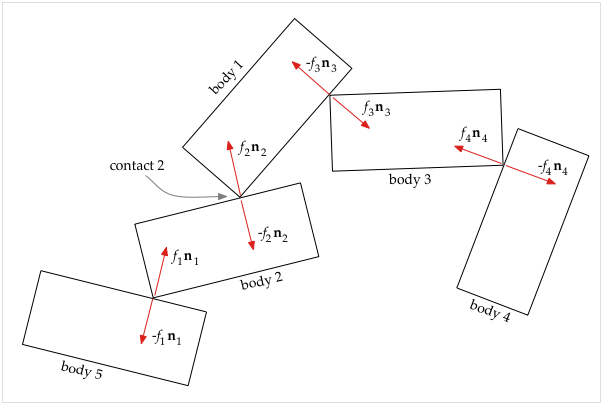
5 bodies, 4 contact points, 8 contact forces

To illustrate how the A matrix and the b vector are calculated, consider the figure above. We have 5 bodies which are in resting contact at 4 contact points and the resulting contact forces are shown. (Note that the normals n_i are always perpendicular to an edge and by convention point out from the object; this determines which forces have minus signs). The contact points are numbered in accord with the contact forces, so that contact force f₁ n₁ is at contact 1, etc. Focusing on contact 2 (between bodies 1 and 2), from equation (2) we can write

d₂'' = a_2,1 f₁ + a_2,2 f₂ + a_2,3 f₃ + a_2,4 f₄ + b₂

(3)

Consider what is affecting the acceleration of the contact distance d₂''. Anything that accelerates body 1 or body 2 can affect d₂''. Here is a list of these sources of acceleration of d₂'' and where they wind up in equation (3).

For all the non-contact forces (gravity, thrust, etc.) currently acting on body 1, we calculate what is the resulting acceleration of the corner of body 1 at contact 2; this is added in to b₂.
Similarly, for all the non-contact forces (gravity, thrust, etc.) currently acting on body 2, we calculate what is the resulting acceleration of the point on body 2 at contact 2; this is added in to b₂.
Regarding contact force f₁ n₁, for a unit change in f₁ we calculate what would be the resulting acceleration of the point on body 2 at contact 2; this is put in a_2,1.
Regarding contact force f₂ n₂, for a unit change in f₂ we calculate what would be the resulting acceleration of the corner of body 1 at contact 2; this is put in a_2,2.
Regarding contact force −f₂ n₂, for a unit change in f₂ we calculate what would be the resulting acceleration of the point on body 2 at contact 2; this is added to a_2,2.
Regarding contact force −f₃ n₃, for a unit change in f₃ we calculate what would be the resulting acceleration of the corner of body 1 at contact 2; this is put in a_2,3.
Because contact forces f₄ n₄ and −f₄ n₄ do not directly affect bodies 1 or 2 we set a_2,4 = 0.

I hope this gives you some idea of how the A matrix and the b vector are calculated. Complete details on these calculations are given below in the sections Calculating the A Matrix and Calculating the b Vector.

Once we have found the A matrix and b vector, we are ready to solve equation (1) for the unknown force magnitudes in the f vector, subject to the following 3 constraints:

a_i >= 0, f_i >= 0, a · f = 0

(4)

The constraints in words are:

a_i >= 0 means we disallow interpenetration (which occurs when a_i < 0). We require all the relative normal accelerations between bodies at contact points to be either zero (in contact) or positive (separating).
f_i >= 0 means we require contact forces to be zero or positive because they can only push, not pull.
a · f = 0 means that, at every contact point, if there is a contact force then acceleration is zero OR if there is acceleration (separation) then there is no contact force. The dot in the equation is the vector dot product.

The paper Fast contact force computation for nonpenetrating rigid bodies. by David Baraff goes into full detail about how to solve equation (1) subject to the constraints (4). I'll give a quick description here of how the algorithm described in that paper works.

The algorithm begins by setting all the contact forces in f to zero. The basic idea is to add in one contact force at a time, adding just enough force to maintain the constraints, and readjusting the other forces as necessary. We ignore the contact points we haven't yet considered, gradually increasing the set of contact points that obey the constraints. Here is a very simplified sketch of how it works:

Begin by considering only contact 1, ignoring all other contact points (which are likely violating the constraint that a_i >= 0). We calculate the amount of force f₁ at contact point 1 which is just sufficient to make a₁ = 0.
Next add in contact 2. Solve for f₂, adjusting f₁ as necessary, so that the three constraints are valid for a₁, a₂ and f₁, f₂.
Continue adding in contacts and contact forces one at a time, while adjusting previous forces as necessary to maintain the three constraints (4).

At each point we are solving a subset of the matrix equation (1) involving only those contact points that we have considered so far. By the final step we have added in all of the contact points and therefore have a complete solution of equation (1) which obeys the constraints (4).

Now that we know the contact forces, the last step is to apply them to the bodies, which gives the final set of body accelerations that the evaluate method then returns to the differential equation solver. The geometry of where each contact force is applied on each body comes into play here to determine how that contact force affects the linear and angular acceleration of a given body. This process is very similar to that described on the Rigid Body Collisions web page for treatment of forces such as the thrust force.

The differential equation solver then continues to evolve the simulation over time using those new accelerations. These accelerations have however been precisely calculated so that the bodies that are in resting contact remain in resting contact without interpenetrating.

Calculating the A Matrix

Our goal here is to calculate the entries of the A matrix of equation (1). As described above, the i, j-th entry in the A matrix, a_{i j}, specifies how the j-th contact force, f_j, affects the acceleration of the i-th contact distance, d_i''.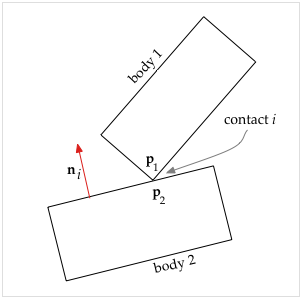

2 bodies in contact

For a particular contact point i, let the bodies be numbered 1 and 2, with body 2 specifying the normal vector n_i pointing out from body 2 towards body 1 (as in the diagram above). Let p₁ be the point on body 1 that is in contact with the point p₂ on body 2. Let d_i be the distance between p₁ and p₂. If we regard p₁ and p₂ as vectors from the origin to those points on bodies 1 and 2, then their difference (p₁ − p₂) is also a vector and we can write

d_i = n_i ⋅ (p₁ − p₂)

(5)

because the dot product with the normal gives us the component of the vector (p₁ − p₂) in the direction of n. Note that d_i is therefore a scalar quantity. Keeping in mind that all of the variables in equation (5) are functions of time, we can take the derivative twice as follows: d_i' = n_i' ⋅ (p₁ − p₂) + n_i ⋅ (p₁' − p₂')
d_i'' = n_i'' ⋅ (p₁ − p₂) + 2 n_i' ⋅ (p₁' − p₂') + n_i ⋅ (p₁'' − p₂'') Because this is a point of contact, we have that p₁ − p₂ = 0 so the above simplifies to

d_i'' = n_i ⋅ (p₁'' − p₂'') + 2 n_i' ⋅ (p₁' − p₂')

(6)

The second term, 2 n_i' ⋅ (p₁' − p₂'), is velocity dependent (so you can immediately calculate it without knowing the forces involved), and is therefore part of b_i. See Calculating the b Vector below. So the f_j dependent part of equation (6) is just

n_i ⋅ (p₁'' − p₂'').

(7)

A contact force f_j n_j only affects d_i'' if that contact force operates on body 1 or body 2. If that is not the case, we know that a_{i j} = 0. Assume now that f_j n_j affects body 1 or body 2. But keep in mind that f_j n_j may be a contact force that is not at the i-th contact point (see the earlier diagram of 5 bodies in contact for example). We can find a_{i j} from the geometry of the situation as follows.

Let n_j be the vector normal at the j-th contact point. Assume that the j-th contact involves body 1. Then the contact force is f_j n_j if the contact involves a corner of body 1 or −f_j n_j if the contact involves an edge of body 1. From the geometry we can calculate the effect of the force on body 1, and therefore on the acceleration of p₁''. If the contact involves body 2, then the effect is on p₂''. Then using equation (7) we will arrive at the contribution of f_j n_j to a_{i j}.

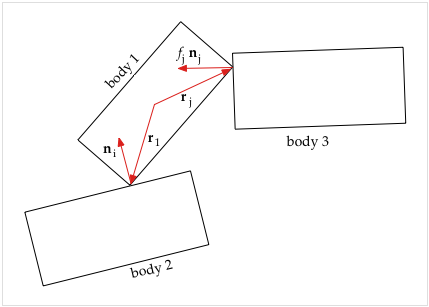
3 bodies in contact

Define the following additional variables:

x₁ = center of mass of body 1
r₁ = vector from center of mass of body 1 to p₁ at the i-th contact point
r_j = vector from center of mass of body 1 to the j-th contact point
ω₁ = magnitude of the angular velocity of body 1
ω₁ = angular velocity of body 1, a vector that is perpendicular to the plane, so ω₁ = {0, 0, ω₁}.
v₁ = x₁' = velocity vector of center of mass of body 1
m₁ = mass of body 1

Then p₁ = x₁ + r₁ and, recognizing that all these variables are functions of time, we can take derivatives:

p₁' = x₁' + r₁' = v₁ + ω₁ × r₁

(7a)

Here we used the knowledge that r₁ is only changing by rotation at a rate of ω₁. An elementary bit of calculus then gives the result that r₁' = ω₁ × r₁ where the × indicates vector cross product. Taking another derivative: p₁'' = v₁' + ω₁' × r₁ + ω₁ × r₁'

p₁'' = v₁' + ω₁' × r₁ + ω₁ × (ω₁ × r₁)

(8)

The term ω₁ × (ω₁ × r₁) is velocity dependent, so it goes into the b vector. The f_j dependent part of p₁'' is therefore

v₁' + ω₁' × r₁

(8a)

Our task now is to find out how much a unit change in f_j affects this.

Because v₁' is the linear acceleration of body 1, we have by Newton's First Law v₁' = (total force on body 1) /m₁ Therefore the f_j dependent part of v₁' is f_j n_j /m₁ Because we are working in 2D, we can write angular acceleration as ω₁' = τ₁ / I₁ where τ₁ = torque on body 1, and I₁ = rotational inertia of body 1 about the center of mass. (If you are working in 3D, angular acceleration has another term; see [Baraff-1] for more information). Suppose that the j-th contact occurs at the point p_j, and the vector r_j goes from center of mass of object 1 to p_j. Then the force f_j n_j contributes a torque of r_j × f_j n_j. So the f_j dependent part of ω₁' is (r_j × f_j n_j) / I₁ and we can write equation (8a), the f_j dependent part of p₁'', as f_j n_j / m₁ + (r_j × f_j n_j) × r₁ / I₁
= f_j (n_j / m₁ + (r_j × n_j) × r₁ / I₁) and the f_j dependent part of d_i'' in equation (6) is then f_j n_i ⋅ (n_j / m₁ + (r_j × n_j) × r₁ / I₁) Therefore, looking back at equation (2) for context, we have the dependence of d_i'' on f_j as

n_i ⋅ (n_j / m₁ + (r_j × n_j) × r₁ / I₁)

(9)

which goes into a_{i j}.

Keep in mind that we assumed that f_j n_j affected body 1. If instead it is −f_j n_j affecting body 1, then that changes the sign of expression (9). If f_j n_j affects body 2 instead of body 1, then the effects are on p₂'' in equation (6), so there is a sign change and also we use m₂, r₂, and I₂ in expression (9) and r_j is computed relative to body 2. Also, in the case where f_j n_j is at a contact point between bodies 1 and 2, then f_j n_j affects body 1 and −f_j n_j affects body 2 and you wind up using expression (9) twice and putting the sum in a_{i j}.

Calculating the b Vector

Here we calculate the b vector of equation (1). The b vector specifies what the contact distance acceleration d_i'' would be in the absence of contact forces. It depends on non-contact forces such as gravity, thrust, rubber band force, damping, etc., but also has a velocity dependent component.

Note that it is these forces that cause the contact forces to exist; the contact forces develop in reaction to the other forces that are pushing the objects together, so contact forces are also known as "reaction forces".

In the context of solving equation (1), the b vector is regarded as a "constant" vector, because at the moment in time that we are solving equation (1) for the contact forces, the b vector is a known quantity.

2 bodies in contact

We continue with the same scenario and variables defined in the previous section Calculating the A Matrix. That is, we consider the i-th contact, and we number the bodies as 1 and 2, where body 2 determines the normal vector n_i of the contact. We are seeking an expression for b_i in equation (2). We start from equation (6) which was derived in the previous section: d_i'' = n_i ⋅ (p₁'' − p₂'') + 2 n_i' ⋅ (p₁' − p₂') We first consider the term 2 n_i'⋅ (p₁' - p₂'). It is dependent only on current velocity, not acceleration, and so is independent of any contact forces being applied, and therefore belongs in the b vector. Recall n_i is the normal of body 2. Therefore, if body 2 is stationary (a wall or floor for example) then its normal does not change, so n_i' is the zero vector and this term is zero.

Derivation of n_i'.
Recall that n_i is the normal vector to body 2 in the scenario of the previous section. We know that body 2 is rotating with angular velocity ω₂. Therefore, by an elementary bit of calculus we can write n_i' = ω₂ × n_i where we treat angular velocity as a vector ω₂ perpendicular to the plane so that ω₂ = {0, 0, ω₂} Here is the derivation of that result: Let n_i be defined as follows (because we are in 2D the z component is zero): n_i = {n_ix, n_iy, 0} We know that the vector n_i is rotating at a rate ω₂. Ignoring any acceleration, we could write the vector n_i as a function of time like this: n_i = |n_i| {cos(ω₂ t), sin(ω₂ t), 0} Where |n_i| is the magnitude of the vector n_i, and t = time. The first derivative is then n_i' = |n_i| {−ω₂ sin(ω₂ t), ω₂ cos(ω₂ t), 0} which is equivalent to: n_i' = {−ω₂ n_iy, ω₂ n_ix, 0} which can also be expressed as a cross product of the two vectors: n_i' = ω₂ × n_i
Now we can use that expression for n_i' and equation (7a) which gives an expression for p₁' (and similarly for p₂' as well) to write that

2 n_i' ⋅ (p₁' − p₂') = 2 (ω₂ × n_i) ⋅ (v₁ + ω₁ × r₁ − (v₂ + ω₂ × r₂))

(10)

The above expression is part of equation (6), and is added in to b_i. But only in the case where body 2 is a moving object; if body 2 is stationary (a wall or floor for example), then n_i' is zero.

Next consider the term n_i ⋅ (p₁'' − p₂'') of equation (6). We need to include in b_i the effect of any non-contact forces on the accelerations of the contact points p₁ and p₂. We will start from equation (8) which was derived in the previous section: p₁'' = v₁' + ω₁' × r₁ + ω₁ × (ω₁ × r₁) It turns out that the accelerations v₁' and ω₁' that are due to non-contact forces have already been calculated for us by the earlier processes (see evaluate method of Thruster5 class). Those accelerations are passed in to our evaluate method and so we simply plug them into equation (8) to get p₁'' (and p₂'' has the similar expression). So we can write this out as

n_i ⋅ (p₁'' − p₂'') = n_i ⋅ (v₁' + ω₁' × r₁ + ω₁ × (ω₁ × r₁) &minus (v₂' + ω₂' × r₂ + ω₂ × (ω₂ × r₂)))

(11)

which is part of equation (6) to be added in to b_i. Keep in mind that in the above equation, v₁' and ω₁' are the accelerations of body 1 due only to non-contact forces (and similarly for v₂' and ω₂').

We now have in expressions (10) and (11), the contact-force-independent parts of equation (6) which is what goes into b_i.