PhysLab.net – Double Pendulum

This is a simulation of a double pendulum. For large motions it is a chaotic system, but for small motions it is a simple linear system.
You can change parameters in the simulation such as mass, gravity, and length of rods (enable the "show controls" checkbox). You can drag the pendulum with your mouse to change the starting position. If you don't see the simulation try instructions for enabling Java. Scroll down to see the math!

Instructions: click near circles and drag with your mouse

To purchase a professionally
engineered chaotic pendulum,
click here.

For small angles, a pendulum behaves like a linear system (see Simple Pendulum). When the angles are small in the Double Pendulum, the system behaves like the linear Double Spring. In the graph, you can see similar Lissajous curves being generated. This is because the motion is determined by simple sine and cosine functions.

For large angles, the pendulum is non-linear and the phase graph becomes much more complex. You can see this by dragging one of the masses to a larger angle and letting go.

We regard the pendulum rods as being massless and rigid. We regard the pendulum masses as being point masses. The derivation of the equations of motion is shown below, using the direct Newtonian method.

Kinematics of the Double Pendulum

Kinematics means the relations of the parts of the device, without regard to forces. In kinematics we are only trying to find expressions for the position, velocity, & acceleration in terms of the variables that specify the state of the device.

x = horizontal position of pendulum mass
y = vertical position of pendulum mass
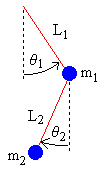
θ = angle of pendulum (0 = vertical downwards, counter-clockwise is positive)
L = length of rod (constant)

We place the origin at the pivot point of the upper pendulum. We regard y as increasing upwards. We indicate the upper pendulum by subscript 1, and the lower by subscript 2. Begin by using simple trigonometry to write expressions for the positions x₁, y₁, x₂, y₂ in terms of the angles θ₁, θ₂. x₁ = L₁ sin θ₁ y₁ = −L₁ cos θ₁ x₂ = x₁ + L₂ sin θ₂ y₂ = y₁ − L₂ cos θ₂ The velocity is the derivative with respect to time of the position. x₁' = θ₁' L₁ cos θ₁ y₁' = θ₁' L₁ sin θ₁ x₂' = x₁' + θ₂' L₂ cos θ₂ y₂' = y₁' + θ₂' L₂ sin θ₂ The acceleration is the second derivative.

x₁'' = −θ₁'² L₁ sin θ₁ + θ₁'' L₁ cos θ₁

(1)

y₁'' = θ₁'² L₁ cos θ₁ + θ₁'' L₁ sin θ₁

(2)

x₂'' = x₁'' − θ₂'² L₂ sin θ₂ + θ₂'' L₂ cos θ₂

(3)

y₂'' = y₁'' + θ₂'² L₂ cos θ₂ + θ₂'' L₂ sin θ₂

(4)

Forces in the Double Pendulum

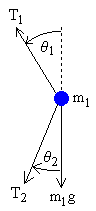
upper mass

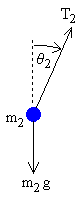
forces in lower mass of double pendulum

lower mass

We treat the two pendulum masses as point particles. Begin by drawing the free body diagram for the upper mass and writing an expression for the net force acting on it. Define these variables:

T = tension in the rod
m = mass of pendulum
g = gravitational constant

The forces on the upper pendulum mass are the tension in the upper rod T₁, the tension in the lower rod T₂, and gravity −m₁ g. We write separate equations for the horizontal and vertical forces, since they can be treated independently. The net force on the mass is the sum of these. Here we show the net force and use Newton's law F = m a.

m₁ x₁'' = −T₁ sin θ₁ + T₂ sin θ₂

(5)

m₁ y₁'' = T₁ cos θ₁ − T₂ cos θ₂ − m₁ g

(6)

For the lower pendulum, the forces are the tension in the lower rod T₂, and gravity −m₂ g.

m₂ x₂'' = −T₂ sin θ₂

(7)

m₂ y₂'' = T₂ cos θ₂ − m₂ g

(8)

In relating these equations to the diagrams, keep in mind that in the example diagram θ₁ is positive and θ₂ is negative, because of the convention that a counter-clockwise angle is positive.

Direct Method for Finding Equations of Motion

Now we do some algebraic manipulations with the goal of finding expressions for θ₁'', θ₂'' in terms of θ₁, θ₁', θ₂, θ₂'. Begin by solving equations (7), (8) for T₂ sin θ₂ and T₂ cos θ₂ and then substituting into equations (5) and (6).

m₁ x₁'' = −T₁ sin θ₁ − m₂ x₂''

(9)

m₁ y₁'' = T₁ cos θ₁ − m₂ y₂'' − m₂ g − m₁ g

(10)

Multiply equation (9) by cos θ₁ and equation (10) by sin θ₁ and rearrange to get

T₁ sin θ₁ cos θ₁ = −cos θ₁ (m₁ x₁'' + m₂ x₂'')

(11)

T₁ sin θ₁ cos θ₁ = sin θ₁ (m₁ y₁'' + m₂ y₂'' + m₂ g + m₁ g)

(12)

This leads to the equation

sin θ₁ (m₁ y₁'' + m₂ y₂'' + m₂ g + m₁ g) = −cos θ₁ (m₁ x₁'' + m₂ x₂'')

(13)

Next, multiply equation (7) by cos θ₂ and equation (8) by sin θ₂ and rearrange to get

T₂ sin θ₂ cos θ₂ = −cos θ₂ (m₂ x₂'')

(14)

T₂ sin θ₂ cos θ₂ = sin θ₂ (m₂ y₂'' + m₂ g)

(15)

which leads to

sin θ₂ (m₂ y₂'' + m₂ g) = −cos θ₂ (m₂ x₂'')

(16)

Next we need to use a program such as Mathematica to solve equations (13) and (16) for θ₁'', θ₂'' in terms of θ₁, θ₁', θ₂, θ₂'. Note that we also include the definitions given by equations (1-4), so that we have 2 equations (13, 16) and 2 unknowns (θ₁'', θ₂''). The result is somewhat complicated, but is easy enough to program into the computer.

θ₁'' =	−g (2 m₁ + m₂) sin θ₁ − m₂ g sin(θ₁ − 2 θ₂) − 2 sin(θ₁ − θ₂) m₂ (θ₂'² L₂ + θ₁'² L₁ cos(θ₁ − θ₂))
	L₁ (2 m₁ + m₂ − m₂ cos(2 θ₁ − 2 θ₂))

θ₂'' =	2 sin(θ₁ − θ₂) (θ₁'² L₁ (m₁ + m₂) + g(m₁ + m₂) cos θ₁ + θ₂'² L₂ m₂ cos(θ₁ − θ₂))
	L₂ (2 m₁ + m₂ − m₂ cos(2 θ₁ − 2 θ₂))

These are the equations of motion for the double pendulum.

Numerical Solution

The above equations are now close to the form needed for the Runge-Kutta method. The final step is convert these two 2nd order equations into four 1st order equations. Define the first derivatives as separate variables:

ω₁ = angular velocity of top rod
ω₂ = angular velocity of bottom rod

Then we can write the four 1st order equations: θ₁' = ω₁ θ₂' = ω₂

ω₁' =	−g (2 m₁ + m₂) sin θ₁ − m₂ g sin(θ₁ − 2 θ₂) − 2 sin(θ₁ − θ₂) m₂ (ω₂² L₂ + ω₁² L₁ cos(θ₁ − θ₂))
	L₁ (2 m₁ + m₂ − m₂ cos(2 θ₁ − 2 θ₂))

ω₂' =	2 sin(θ₁−θ₂) (ω₁² L₁ (m₁ + m₂) + g(m₁ + m₂) cos θ₁ + ω₂² L₂ m₂ cos(θ₁ − θ₂))
	L₂ (2 m₁ + m₂ − m₂ cos(2 θ₁ − 2 θ₂))

This is now exactly the form needed to plug in to the Runge-Kutta method for numerical solution of the system.