PhysLab.net – Simple Pendulum

This simulation shows a simple pendulum operating under gravity. For small oscillations the pendulum is linear, but it is non-linear for larger oscillations.
You can change parameters in the simulation such as mass, gravity, and friction (damping). You can drag the pendulum with your mouse to change the starting position. If you don't see the simulation try instructions for enabling Java. Scroll down to see the math!

Puzzles

Try using the graph and changing parameters like mass, length, gravity to answer these questions about the spring simulation:

What is the relationship between angular acceleration and angle?
How do mass, length, or gravity affect the relationship between angular acceleration and angle?
For small oscillations, how do length or gravity affect the period or frequency of the oscillation?

Note: Leave damping and drive frequency set to zero here (they complicate things). You'll find the answers below. (Hint: Try starting the pendulum from an almost vertically "up" position.)

Physics - Rotational Method

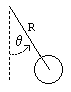
pendulum variables

The pendulum is modeled as a point mass at the end of a massless rod. We define the following variables:

θ = angle of pendulum (0=vertical)
R = length of rod
T = tension in rod
m = mass of pendulum
g = gravitational constant

We will derive the equation of motion for the pendulum using the rotational analog of Newton's second law for motion about a fixed axis, which is τ = I α where

τ = net torque
I = rotational inertia
α = θ''= angular acceleration

The rotational inertia about the pivot is I = m R². Torque can be calculated as the vector cross product of the position vector and the force. The magnitude of the torque due to gravity works out to be τ = −R m g sin θ. So we have −R m g sin θ = m R² α which simplifies to

θ'' = − ^g⁄_R sin θ

(1)

This is the equation of motion for the pendulum.

Physics - Direct Method

Most students are less familiar with rotational inertia and torque than with the simple mass and acceleration found in Newton's second law, F = m a. To show that there is nothing new in the rotational version of Newton's second law, we derive the equation of motion here without the rotational dynamics. As you will see, this method involves more algebra.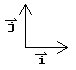

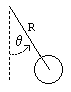
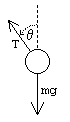
pendulum forces

We'll need the standard unit vectors, i, j. We use bold and overline to indicate a vector.

i = unit vector in horizontal direction
j = unit vector in vertical direction

The kinematics of the pendulum are then as follows position = R sin θ i − R cos θ j velocity = R θ' cos θ i + R θ' sin θ j
acceleration = R(θ'' cos θ i − θ' ² sin θ i + θ'' sin θ j + θ' ² cos θ j) The position is derived by a fairly simple application of trigonometry. The velocity and acceleration are then the first and second derivatives of the position.

Next we draw the free body diagram for the pendulum. The forces on the pendulum are the tension in the rod T and gravity. So we can write the net force as: F = T cos θ j − T sin θ i − m g j

Using Newton's law F = m a and the pendulum acceleration we found earlier, we have T cos θ j − T sin θ i − m g j = m R(θ'' cos θ i − θ' ² sin θ i + θ'' sin θ j + θ' ² cos θ j) We can write the vector components of the above equation as separate equations. This gives us two simultaneous equations: the first for the i component and the second for the j component. −T sin θ = m R(θ'' cos θ − θ' ² sin θ) T cos θ − m g = m R(θ'' sin θ + θ' ² cos θ) Next we do some algebraic manipulations to eliminate the unknown T. Multiply the first equation by cos θ and the second by sin θ. −T sin θ cos θ = m R(θ'' cos²θ − θ' ² sin θ cos θ) T cos θ sin θ − m g sin θ = m R(θ'' sin²θ + θ' ² sin θ cos θ) Use the first equation to substitute for T cos θ sin θ in the second equation and do a little more algebra to get: −θ'' cos²θ + θ' ² sin θ cos θ = θ'' sin²θ + θ' ² sin θ cos θ + ^g⁄_R sin θ With the trig identity cos²θ + sin²θ = 1 this simplifies to equation (1) θ'' = − ^g⁄_R sin θ

Physics - Energy Method

There is yet a third way to derive the equations of motion for the pendulum. This is to use the "indirect" energy based method associated with the terms "Lagrangian", "Euler-Lagrange equations", "Hamiltonian", and others. While this method isn't shown here, you can see an example of it for the Pendulum+Cart simulation.

Numerical Solution

To solve the equations of motion numerically, so that we can drive the simulation, we use the Runge-Kutta method for solving sets of ordinary differential equations. First we define a variable for the angular velocity ω = θ'. Then we can write the second order equation (1) as two first order equations. θ' = ω ω' = − ^g⁄_R sin θ This is the form needed for using the Runge-Kutta method.

Puzzle Answers

Question: What is the relationship between angular acceleration and angle?

Answer: It is a sine wave relationship as given by equation (1): θ'' = − ^g⁄_R sin θ

Question: How do mass, length, or gravity affect the relationship between angular acceleration and angle?

Answer: From equation (1) we see that:

Mass doesn't affect the motion at all.
The amplitude of the sine relationship is proportional to gravity.
The amplitude of the sine relationship is inversely proportional to length of the pendulum.

Question: For small oscillations, how do length or gravity affect the period or frequency of the oscillation?

Answer: For small oscillations we can use the approximation that sin θ = θ. Then the equation of motion becomes θ'' = − ^g⁄_R θ This is a linear relationship. You can see that the graph of acceleration versus angle is a straight line for small oscillations. This is the same form of equation as for the single spring simulation. The analytic solution is $\theta(t) = \theta_0 \cos(\sqrt{g/R} \; t)$ where θ₀ is the initial angle and t is time. The period is the time it takes for θ(t) to repeat, so period = $\frac{2 \pi}{\sqrt{g/R}}$ The frequency of oscillation is the inverse of the period: frequency = $\frac{1}{2 \pi} \sqrt{g/R}$ So we predict that

increasing length by 4 times doubles the period and halves the frequency;
increasing gravity by 4 times halves the period and doubles the frequency;